XSMath

Mathematics and Statistics Resources

Differentiation

First Principle of Differentiation

$f'(x)= \lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

Properties of Derivatives

$\frac{d}{dx}c=0$ Where $c$ is a constant

$\frac{d}{dx}[cf(x)]=c\frac{d}{dx}f(x)$ or $(cf)'=cf'$

$\frac{d}{dx}[f(x)+g(x)]=\frac{d}{dx}f(x)+\frac{d}{dx}g(x)$

$\frac{d}{dx}[f(x)-g(x)]=\frac{d}{dx}f(x)-\frac{d}{dx}g(x)$

Exponents

$\frac{d}{dx}(x)=1$

$\frac{d}{dx}(x^n)=nx^{n-1}$

Exponential Fuctions

$\frac{d}{dx}(e^x)=e^x$

$\frac{d}{dx}(a^x)=a^xlna$

$\frac{d}{dx}(lnx)=\frac{1}{x}$

Trigonometric Functions

$\frac{d}{dx}(\sin x)=\cos x$

$\frac{d}{dx}(\cos x)=-\sin x$

$\frac{d}{dx}(\tan x)=\sec^2x$

$\frac{d}{dx}(\csc x)=-\csc x\cot x$

$\frac{d}{dx}(\sec x)=\sec x\tan x$

$\frac{d}{dx}(\cot x)=-\csc^2x$

Inverse trigonometric functions 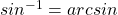$sin^{-1}=arcsin$

$\frac{d}{dx}(\sin^{-1}x)=\frac{1}{\sqrt{1-x^2}}$

$\frac{d}{dx}(\cos^{-1}x)=-\frac{1}{\sqrt{1-x^2}}$

$\frac{d}{dx}(\tan^{-1}x)=\frac{1}{1+x^2}$

$\frac{d}{dx}(\csc^{-1}x)=-\frac{1}{|x|\sqrt{x^2-1}}$

$\frac{d}{dx}(\sec^{-1}x)=\frac{1}{|x|\sqrt{x^2-1}}$

$\frac{d}{dx}(\cot^{-1}x)=-\frac{1}{1+x^2}$

Hyperbolic Functions

$\frac{d}{dx}(\sinh x)=\cosh x$

$\frac{d}{dx}(\cosh x)=\sinh x$

$\frac{d}{dx}(\tanh x)=sech{^2} x$

$\frac{d}{dx}(\csch x)=-\csch x\coth x$

$\frac{d}{dx}(\sech x)=-\sech x\tanh x$

$\frac{d}{dx}(\coth x)=-csch ^2 x$

Chain Rule

The composite function $F=f\circ{g}$ defined by $F(x)=f(g(x))$

$\frac{d}{dx}(f[g(x)])=\frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx}$ or

$F'(x)=f'(g(x))\cdot{g'(x)}$

Product Rule

$\frac{d}{dx} [f(x)g(x)]=f(x)\frac{d}{dx}[g(x)]+g(x)\frac{d}{dx}[f(x)]$ or

$(fg)'=fg'+gf'$

Quotient Rule

$\frac{d}{dx}[\frac{f(x)}{g(x)}]=\frac{g(x)\frac{d}{x}[f(x)]-f(x)\frac{d}{dx}[g(x)]}{[g(x)]^2}$ or

$(\frac{f}{g})'=\frac{gf'-fg'}{g^2}$

Video Links