Polynomials | XSMath

A polynomial of degree $n$ has the form:

$P(x)=a_nx^n+a_{n-1}x^{n-1}+ \cdots +a_1x+a_0$

Long Division Polynomials

$\frac{x^2+7x-9}{x+2}$

Write in long division format

$x+2 \overline{\smash{\big)}x^2+7x-9}$

Divide the leading term of the dividend by the leading term of the divisor $\frac{x^2}{x}=x$

Write $x$ at the top and multiply by $x+2$ . Subtract from divident.

$\begin{array}{c} x \\ x+2{\overline{\smash{\big)}\,x^2+7x-9\phantom{)}}}\\ \underline{-~\phantom{(}(x^2+2x)\phantom{-b)}}\\ 0+5x-9\phantom{)}\\ \end{array}$

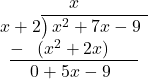
Divide the leading term of the obtained remainder by the leading term of the divisor $\frac{5x}{x}=5$

Write $+5$ at the top and multiply by $x+2$ . Subtract from divident.

$\begin{array}{c} x+5 \\ x+2{\overline{\smash{\big)}\,x^2+7x-9\phantom{)}}}\\ \underline{-~\phantom{(}(x^2+2x)\phantom{-b)}}\\ 0+5x-9\phantom{)}\\ \underline{-~\phantom{()}(5x+10)}\\ 0-19\phantom{)} \end{array}$

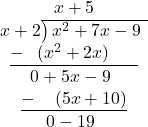
Divide the obtained remainder by the divisor and add to the answer.

Therefore:

$\frac{x^2+7x-9}{x+2}=x+5+\frac{-19}{x+2}$